Day

This module provides a good understanding of linear algebra concepts / matrix computations by hand, practical algebraic concepts and methods that are useful in data analysis applications, links  between  vector  space  representations  and  matrices,  and  between decompositions such as eigenvalue decomposition, singular value decomposition, linear systems, least squares solutions. To provide a working understanding of matrices and vector spaces for later modules to build on and to teach students practical techniques and algorithms for fundamental matrix operations and solving linear equations.

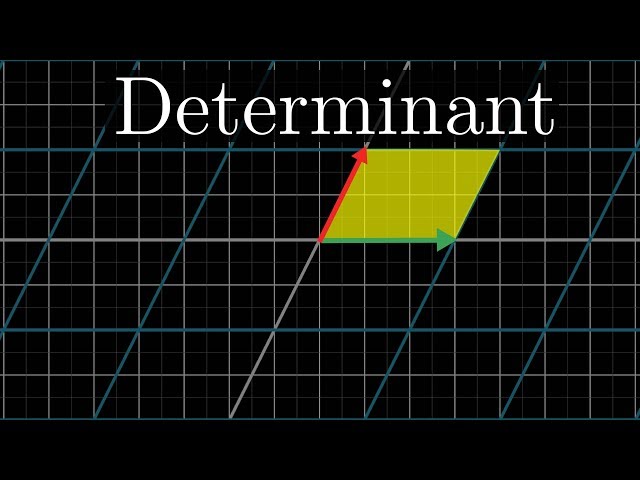
They must also understand the equivalence of linear maps between vector spaces and matrices and be able to row reduce a matrix, compute its rank and solve systems of linear equations. The definition of a determinant in all dimensions will be given in detail, together with applications and techniques for calculating determinants. Students must know the definition of the eigenvalues and eigenvectors of a linear map or matrix, and know how to calculate them.